Quizlet

USATestprep Review #2 Wrong Answers

USATestprep Review #1 Wrong Answers

Transformations

Transformation Game

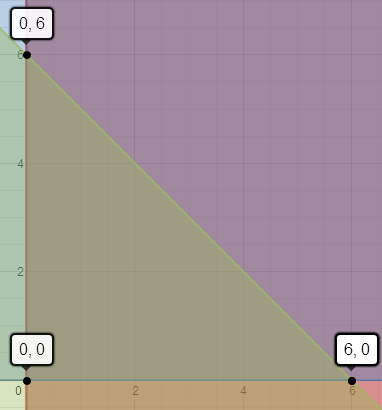
Linear Programming

Vertices:	(0,6)		(0,0)		(6,0)
Constraints	Objective Function: 3x + 4y
x ≥ 0 y ≥ 0 x + y ≤ 6	24	0		18

Vertices:	(-5,4)		(0,6)		(0,4)
Constraints	Objective Function: 2x + 5y
x ≤ 5 y ≥ 4 -2x + 5y ≤ 30	10	30		20

Vertices:	(1,8)		(1,2)		(5,2)
Constraints	Objective Function: 7x + 3y
x ≥ 1 y ≥ 2 6x + 4y ≤ 38	31	13		41

Vertices:	(0,8)		(0,4)		(6,8)
Constraints	Objective Function: 4x + 6y
x ≥ 0 y ≤ 8 -2x + 3y ≥ 12	48	24		72

Vertices:	(0,0)		(0,5)		(2,3)		(8,0)
Constraints	Objective Function: 8x + 7y
x ≥ 0 y ≥ 0 4x + 4y ≤ 20 x + 2y ≤ 8	0	35		37		64

Vertices:	(0,4)		(0,2)		(3,0)		(4,3)
Constraints	Objective Function: 3x + 5y
x ≥ 0 2x +3y ≥ 6 3x - y ≤ 9 x +4y ≤ 16	20	10		9		27

Statistics Test

Statistics Test

Compound Interest Formula

Compound Interest: Interest calculated on the initial principal and also on the accumulated interest of previous periods of a deposit or loan.

 

P = principal amount (the initial amount you borrow or deposit)

r  = annual rate of interest (as a decimal)

t  = number of years the amount is deposited or borrowed for.

n  =  number of times the interest is compounded per year 

Statistics

Statistics Data

Graphing Exponential Growth/Decay

• Graphing Exponential Growth/Decay

1. Create the Parent Graph.

2. Identify A,H,K.

3. Create your new T-Chart.

• Domain: All real #'s.
• Range: y>k; when a is positive. y<k; when a is negative.
• Asymptote: y=k.

4. Draw Asymptote.

5. Graph new points.

• Exponential Formula:  y=a×b^x-h+k
• a = multiplier.

a>1 = stretch
0<a<1 = compression
a< 0(negative) = flipped over x-axis.

• b = base

b>1 = whole #, growth, always increasing.

0<b<1 = fraction; decay, always decreasing.

B is never negative only the multiplier is.

• h = lf/rt; opposite
• k = up/dn

General Forms of a Sequence

GENERAL FORMS OF A SEQUENCE

Sequence- Is an ordered list of terms or elements.

Arithmetic  sequence formula- In an Arithmetic Sequence the difference between one term and the next is a constant. Also called the Common Difference. 

Geometric sequence formula-  In a Geometric Sequence each term is found by multiplying the previous term by a constant. Also called the Common Ratio.

Example:

2, 4, 8, 16, 32, 64, 128, 256, ...

This sequence has a factor of 2 between each number. Each term (except the first term) is found by multiplying the previous term by 2.

Finite sequence- Is a function with domain 1,2,3.

Infinite sequence- Is a function with domain 1,2,3,4.... etc.

Series- Is the sum of a sequence.

Explicit formula-  Each domain is an answer not based on any values.

Recursive Formula-  Each domain is a answer based on a previous answer.

Characteristics and Traits of a Graph

The descriptions for each is posted below.

Domain- X-Values

Range- Y-Values

End Behavior- Describing the two ends of the graph. While X approaches negative infinity, Y approaches negative infinity. While X approaches positive infinity, Y approaches positive infinity and vice versa in another situation.

x→∞, y→∞. x→-∞,y→-∞

Absolute Max/Min- 1 point that has the highest/lowest point on a graph. 

A specific point on the graph.

Local Max/Min- More than 1 point on a graph at its highest/lowest point.

Interval of Increase- Section of a graph where the y-values increase.

Interval of Decrease- Section of a graph where the y-values decrease.

X-Intercept- Where the line(s) cross over the x-axis.

Y-Intercept- Where the line(s) cross over the y-axis.

Symmetry- Even/Odd/Neither

Even- The graph is symmetrical over the y-axis.

Odd-  The graph is symmetrical about the origin.

Neither- The graph is not symmetrical at all.

Asymptotes- Imaginary line that the graph gets closer and closer too but never touches.

Function- The graph passes the vertical line test. The equation only has 1 x-value per y-value.

One to One- The graph pass the vertical and horizontal line test.